MATERI PERTEMUAN KE 8

Bilangan bulat merupakan suatu bilangan tak pecahan yang terdiri atas

Bilangan bulat positif : 1, 2, 3, 4, . . .

Bilangan nol : 0

Bilangan bulat negatif : . . ., -4, -3, -2, -1

Secara umum, himpunan bilangan bulat dituliskan sebagai  { . . ., -4, -3, -2, -1, 0, 1, 2, 3, 4}. Bilangan bulat dilambangkan dengan Z, yang berasal dari kata “zahlen” (bahasa Jerman) yang berarti bilangan.

Bilangan-bilangan bulat tersebur dapat dituliskan dan diurutkan dalam garis bilangan. Penggunaan garis bilangan saat bermanfaat saat kita melakukan operasi hitung bilangan bulat. Dalam bilangan bulat juga dapat dikelompokkan ke dalam dua bagian yaitu

Bilangan genap : . . ., -6, -4, -2, 0, 2, 4, 6, . . .  Bilangan genap merupakan himpunan bilangan yang jika dibagi 2 bersisa 0.

Bilangan ganjil : . . ., -5, -3, -1, 1, 3, 5, . . . Bilangan ganjil merupakan himpunan bilangan yang jika dibagi 2 bersisa 1 atau -1.

Bilangan Bulat dalam Kehidupan Sehari-hari

Apa saja kegunaan bilangan bulat? Bilangan bulat digunakan dalam kehidupan sehari-hari untuk melakukan perhitungan, mulai dari yang sederhana sampai yang kompleks.

Bilangan bulat juga berfungsi sebagai tipe data dalam bahasa pemrograman komputer.

Contoh Bilangan Bulat

Bilangan bulat dapat disajikan dalam garis bilangan sebagai berikut.

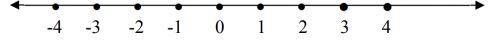
Dalam garis bilangan tersebut, terdapat bilangan bulat yang dikelompokkan dalam beberapa bagian. Pengelompokan bilangan bulat disajikan pada bagian dibawah ini.

Pengelompokan Bilangan Bulat

Bilangan bulat dikelompokkan dalam tiga bagian yaitu bilangan bulat positif, bilangan nol, dan bilangan bulat negatif. Pada bagian ini akan dijelaskan mengenai bilangan bulat positif dan bilangan bulat negatif.

Bilangan Bulat Positif

Bilangan bulat positif adalah himpunan bilangan yang terdiri dari 1, 2, 3, 4, . . . Bilangan bulat positif disebut juga dengan bilangan asli.

Bilangan Bulat Negatif

Bilangan bulat negatif adalah himpunan semua bilangan {. . . , -4, -3, -2, -1}. Dalam garis bilangan, bilangan bulat negatif terletak di sebelah kiri angka nol.

Selanjutnya akan dibahas mengenai operasi hitung yang terdapat dalam bilangan bulat.

Operasi Hitung Bilangan Bulat

Beberapa operasi hitung sederhana dalam bilangan bulat antara lain penjumlahan, pengurangan, perkalian, dan pembagian.

Operasi Penjumlahan

Operasi penjumlahan merupakan operasi yang melibatkan tanda “ + “. Dalam garis bilangan, suatu bilangan yang dijumlahkan dengan suatu bilangan positif akan bergerak ke kanan (semakin besar). Berikut akan dijelaskan sifat-sifat dalam operasi penjumlahan.

Sifat Komutatif

Sifat komutatif dapat disebut sebagai sifat pertukaran. Secara umum sifat komutatif yaitu a + b = b + a. Contohnya:

5 + 8 = 8 + 5 = 13

Sifat Asosiatif

Sifat asosiatif disebut juga dengan sifat pengelompokan. Secara umum sifat komutatif dituliskan dengan (a + b) + c = a + (b + c). Contohnya

(4 + 7) + 2 = 4 + (7 + 2) = 13

Sifat identitas terhadap penjumlahan

Unsur identitas terhadap operasi penjumlahan adalah bilangan 0. Mengapa 0 dikatakan sebagai unsur identitas terhadap penjumlahan? Karena jika kita menjumlahkan suatu bilangan dengan 0, hasil operasi penjumlahan akan tetap. Secara umum dituliskan dengan 0 + a = a + 0. Contohnya:

8 + 0 = 0 + 8 = 8

Unsur invers terhadap penjumlahan

Invers (lawan) dari a adalah –a.

Invers (lawan) dari –a adalah a.

Secara umum sifat invers ini dituliskan dengan a + (-a) = 0

Sifat tertutup

Penjumlahan berlaku sifat tertutup artinya penjumlahan bilangan bulat akan menghasilkan bilangan bulat juga. Jika a dan b adalah bilangan maka a + b = c dengan c merupakan bilangan bulat. Contoh:

3 + 8 = 11.  3, 8, 11 merupakan bilangan bulat.

Operasi Pengurangan

Operasi pengurangan merupakan operasi yang melibatkan tanda “ – “. Dalam garis bilangan, suatu bilangan yang dikurangi dengan suatu bilangan positif akan bergerak ke kiri (semakin kecil).

Berikut akan dijelaskan sifat-sifat dalam operasi pengurangan. Untuk suatu bilangan bulat berlaku:

a – b = a + (-b)

a – (-b) = a + b

contoh:

3 – 1 = 3 + (-1) = 2

4 – (-2) = 4 + 2 = 6

Tidak berlaku sifat komutatif dan assosiatif

a – b ≠ b – a

(a – b) – c ≠ a – (b – c)

Contoh:

4 – 2 ≠ 2 – 4

(6 – 2) – 1 ≠ 6 – (2 – 1)

Pengurangan yang melibatkan bilangan 0

a – 0 = a  dan 0 – a = -a

Contoh:

4 – 0 = 4 dan 0 – 4 = -4

Bersifat tertutup

Pengurangan yang melibatkan dua bilangan bulat, hasil operasinya juga merupakan bilangan bulat. Jika a dan b merupakan bilangan bulat, maka a – b = c dengan c merupakan bilangan bulat.

Contoh:

6 – 1 = 5.  6, 1, 5 merupakan bilangan bulat.

Operasi Perkalian

Operasi perkalian merupakan operasi matematika yang melibatkan tanda “×”. Perkalian dapat disebut sebagai penjumlahan yang berulang.

Sifat-sifat operasi perkalian dijelaskan pada bagian berikut.

a x b = ab : hasil perkalian dua bilangan bulat positif merupakan bilangan bulat positif.

Contoh: 5 x 6 = 30.   5, 6, 30 merupakan bilangan bulat positif.

a x (-b) = -ab : hasil perkalian bilangan bulat positif dengan bilangan bulat negative menghasilkan bilangan bulat negatif.

Contoh:  3 x (-4) = -12.  Hasil operasi adalah -12 (bilangan bulat negatif).

(-a) x (-b )= ab : hasil perkalian dua bilangan bulat negatif merupakan bilangan bulat positif.

Contoh:  (-5) x (-2) = 10, menghasilkan bilangan bulat positif yaitu 10.

Sifat komutatif

a x b = b x a

Contoh:  

9 x 2 = 2 x 9 = 18

Sifat assosiatif

(a x b) x c = a x (b x c)

Contoh:

(3 x 2) x 4 = 3 x (2 x 4) = 24

sifat distributif.

a x (b + c) = ab + ac

Contoh:

3 x ( 4 + 2) = (3 x 4) + (3 x 2) = 12 + 6 = 18

Unsur identitas

Unsur identitas terhadap perkalian adalah 1. Perkalian suatu bilangan dengan bilangan 1 akan menghasilkan bilangan itu sendiri.

a x 1 = a

Contoh:

21 x 1 = 21.

Bersifat tertutup

Perkalian dua bilangan bulat menghasilkan bilangan bulat pula.

Jika a dan b bilangan bulat, maka a x b = c dengan c merupakan bilangan bulat.

Contoh:

 7 x 2 = 14.     7, 2, 14 merupakan bilangan bulat.

Operasi Pembagian

Hasil bagi

(+) : (+) = (+)

(+) : (-) = (-)

(-) : (-) = (+)

Hasil bagi bilangan bulat dengan 0 (nol) tidak terdefinisi.

a : 0 = (tidak terdefinisi)

Contoh:

5 : 0 = (tidak terdefinisi)

Tidak berlaku sifat komutatif dan assosiatif.

a : b ≠ b : a

(a : b) : c ≠ a : (b : c)

Contoh:

6 : 2 ≠ 2 : 6

(6 : 3) : 2 ≠ 6 : (3 : 2)

Selanjutnya, coba kerjakan latihan soal berikut. Baca juga Bilangan cacah.

Soal dan Pembahasan

1. Tuliskan himpunan bilangan bulat negatif.

Jawaban: { . . ., -4, -3, -2, -1}

2. Tuliskan sifat-sifat operasi hitung penjumlahan.

Jawaban:

Operasi penjumlahan memiliki sifat-sifat sebagai berikut.

• Komutatif
• Assosiatif
• Identitas
• Invers
• Tertutup

• Disajikan suatu operasi sebagai berikut.

7 x (5 + 3) = (7 x 5) + (7 x 3)

Operasi tersebut melibatkan salah satu sifat dalam operasi perkalian yaitu . . .  .

Jawaban: Sifat Distributif